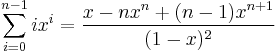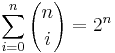Summation
Summation is the operation of combining a sequence of numbers using addition; the result is their sum or total. An interim or present total of a summation process is termed the running total. The numbers to be summed may be integers, rational numbers, real numbers, or complex numbers, and other types of values than numbers can be added as well: vectors, matrices, polynomials, and in general elements of any additive group (or even monoid). For finite sequences of such elements, summation always produces a well-defined sum (possibly by virtue of the convention for empty sums).
Summation of an infinite sequence of values is not always possible, and when a value can be given for an infinite summation, this involves more than just the addition operation, namely also the notion of a limit. Such infinite summations are known as series. Another notion involving limits of finite sums is integration. The term summation has a special meaning related to extrapolation in the context of divergent series.
The summation of the sequence [1, 2, 4, 2] is an expression whose value, the sum of the sequence, is defined to be that of the repeated addition 1 + 2 + 4 + 2, namely 9. Since addition is associative the value does not depend on how the additions are grouped, for instance (1 + 2) + (4 + 2) and 1 + ((2 + 4) + 2) both have the value 9; therefore parentheses are usually omitted in repeated additions. Addition is also commutative, so permuting the terms of a finite sequence does not change its sum. (For infinite summations this property may fail; see absolute convergence for conditions under which it still holds.)
There is no special notation for summation of such explicitly given sequences, as the corresponding repeated addition expression will do (but such an expression does not exist for the summation of an empty sequence; one may substitute "0" for such a summation). If however the terms of the sequence are given by regular pattern, possibly of variable length, then use of a summation operator may be useful or even essential. For the summation of the sequence of consecutive integers from 1 to 100 one could use an addition expression involving an ellipsis to mark out the missing terms: 1 + 2 + 3 + ... + 99 + 100. In this case the reader easily guesses the pattern; however for more complicated patterns, one needs to be precise about the rule used to find successive terms, which can be achieved by using the summation operator "Σ". Using this notation the above summation is written
The value of this summation is 5050. It can be found without performing 99 additions, since it can be shown (for instance by mathematical induction) that
for all natural numbers n. More generally, formulas exist for many summations of terms following a regular pattern.
The term "indefinite summation" refers to the search for an inverse image of a given infinite sequence s of values for the forward difference operator, in other words for a sequence, called antidifference of s, whose finite differences are given by s. By contrast, summation as discussed in this article is called "definite summation".
Contents |
Capital-sigma notation
Mathematical notation uses a symbol that compactly represents summation of many similar terms: the summation symbol ∑ (U+2211), a large upright capital Sigma. This is defined thus:
The subscript gives the symbol for an index variable, i. Here, i represents the index of summation; m is the lower bound of summation, and n is the upper bound of summation. Here i = m under the summation symbol means that the index i starts out equal to m. Successive values of i are found by adding 1 to the previous value of i, stopping when i = n. An example:
 .
.
Informal writing sometimes omits the definition of the index and bounds of summation when these are clear from context, as in
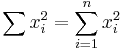 .
.
One often sees generalizations of this notation in which an arbitrary logical condition is supplied, and the sum is intended to be taken over all values satisfying the condition. For example:
is the sum of f(k) over all (integer) k in the specified range,
is the sum of f(x) over all elements x in the set S, and
is the sum of μ(d) over all integers d dividing n.[1]
There are also ways to generalize the use of many sigma signs. For example,
is the same as
A similar notation is applied when it comes to finding multiplicative products; the same basic structure is used, with ∏, or the capital pi, replacing the ∑.
Programming language notation
Summations can also be represented in a programming language. Some languages use a notation for summation similar to the mathematical one. For example, this is Python:
sum(x[m:n+1])
and this is the Perl equivalent of the above Python:
use List::Util 'sum'; sum($m..$n);
and this is the PHP equivalent of the above Python:
$sum = array_sum($x);
and this is Fortran (or MATLAB and Octave):
sum(x(m:n))
and this is Haskell:
sum x
and this is Scheme:
and this is Erlang:
lists:sum(X).
and this is J (or APL):
+/x
and this is TI-BASIC
sum(seq(x,x,m,n[,1])) #text in [brackets] is optional
In other languages loops are used, as in the following Visual Basic/VBScript program:
Sum = 0 For I = M To N Sum = Sum + X(I) Next I
or the following C/C++/C#/Java code, which assumes that the variables m and n are defined as integer types no wider than int, such that m ≤ n, and that the variable x is defined as an array of values of integer type no wider than int, containing at least m − n + 1 defined elements:
int i; int sum = 0; for (i = m; i <= n; i++) { sum += x[i]; }
In some cases a loop can be written more concisely, as in this Perl code:
$sum += $x[$_] for ($m..$n);
or these alternative Ruby expressions:
x[m..n].inject{|a,b| a+b} x[m..n].inject(0){|a,b| a+b}
or in C++, using its standard library:
std::accumulate(&x[m], &x[n + 1], 0)
when x is a built-in array or a std::vector.
Note that most of these examples begin by initializing the sum variable to 0, the identity element for addition. (See "special cases" below).
Also note that the ∑ notation evaluates to a definite value, while most of the loop constructs used above are only valid in an imperative programming language's statement context, requiring the use of an extra variable to hold the final value. It is the variable which would then be used in a larger expression.
The exact meaning of ∑, and therefore its translation into a programming language, changes depending on the data type of the subscript and upper bound. In other words, ∑ is an overloaded symbol.
In the above examples, the subscript of ∑ was translated into an assignment statement to an index variable at the beginning of a for loop. But the subscript is not always an assignment statement. Sometimes the subscript sets up the iterator for a foreach loop, and sometimes the subscript is itself an array, with no index variable or iterator provided. Other times, the subscript is merely a Boolean expression that contains an embedded variable, implying to a human, but not to a computer, that every value of the variable should be used where the Boolean expression evaluates to true.
In the example below:
 is an iterator, which implies a
is an iterator, which implies a foreach loop, but  is a set, which is an array-like data structure that can store values of mixed type. The summation routine for a set would have to account for the fact that it is possible to store non-numerical data in a set.
is a set, which is an array-like data structure that can store values of mixed type. The summation routine for a set would have to account for the fact that it is possible to store non-numerical data in a set.
The return value of ∑ is a scalar in all examples given above.
Special cases
It is possible to sum fewer than 2 numbers:
- If the summation has one summand x, then the evaluated sum is x.
- If the summation has no summands, then the evaluated sum is zero, because zero is the identity for addition. This is known as the empty sum.
These degenerate cases are usually only used when the summation notation gives a degenerate result in a special case. For example, if m = n in the definition above, then there is only one term in the sum; if m > n, then there is none.
Measure theory notation
In the notation of measure & integration theory, a sum can be expressed as a definite integral,
![\sum_{k=a}^b f(k) = \int_{[a,b]} f\,d\mu](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ff0ff2ec229624fa5c2fd9713343b188.png)
where [a,b] is the subset of the integers from a to b, and where μ is the counting measure.
Fundamental theorem of discrete calculus
Indefinite sums can be used to calculate definite sums with the formula[2]:
Approximation by definite integrals
Many such approximations can be obtained by the following connection between sums and integrals, which holds for any:
increasing function f:
decreasing function f:
For more general approximations, see the Euler–Maclaurin formula.
For functions that are integrable on the interval [a, b], the Riemann sum can be used as an approximation of the definite integral. For example, the following formula is the left Riemann sum with equal partitioning of the interval:
The accuracy of such an approximation increases with the number n of subintervals, such that:
Identities
The formulas below involve finite sums; for infinite summations see list of mathematical series
General manipulations
 , where C is a constant
, where C is a constant
Some summations of polynomial expressions
 (See Harmonic number)
(See Harmonic number)
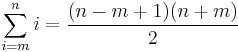 (see arithmetic series)
(see arithmetic series)
 (Special case of the arithmetic series)
(Special case of the arithmetic series)
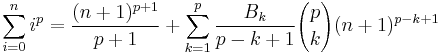 where
where  denotes a Bernoulli number
denotes a Bernoulli number
Some summations involving exponential terms
In the summations below x is a constant unequal to 1
 (m < n; see geometric series)
(m < n; see geometric series)
 (geometric series starting at 1)
(geometric series starting at 1)
 (special case when x = 2)
(special case when x = 2)
 (special case when x = 1/2)
(special case when x = 1/2)
Some summations involving binomial coefficients
There exist enormously many summation identities involving binomial coefficients (a whole chapter of Concrete Mathematics is devoted to just the basic techniques). Some of the most basic ones are the following.
 , the binomial theorem
, the binomial theorem
Growth rates
The following are useful approximations (using theta notation):
 for real c greater than −1
for real c greater than −1 (See Harmonic number)
(See Harmonic number) for real c greater than 1
for real c greater than 1 for nonnegative real c
for nonnegative real c for nonnegative real c, d
for nonnegative real c, d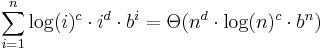 for nonnegative real b > 1, c, d
for nonnegative real b > 1, c, d
See also
- Einstein notation
- Checksum
- Product (mathematics)
- Kahan summation algorithm
- Iterated binary operation
- Summation equation
Notes
- ↑ Although the name of the dummy variable does not matter (by definition), one usually uses letters from the middle of the alphabet (i through q) to denote integers, if there is a risk of confusion. For example, even if there should be no doubt about the interpretation, it could look slightly confusing to many mathematicians to see x instead of k in the above formulae involving k. See also typographical conventions in mathematical formulae.
- ↑ "Handbook of discrete and combinatorial mathematics", Kenneth H. Rosen, John G. Michaels, CRC Press, 1999, ISBN 0-8493-0149-1
Further reading
- Nicholas J. Higham, "The accuracy of floating point summation", SIAM J. Scientific Computing 14 (4), 783–799 (1993).
External links
 Media related to Summation at Wikimedia Commons
Media related to Summation at Wikimedia Commons- Summation on PlanetMath
- Method to Derive Polynomial Representations that Sum Natural Numbers with Exponents
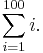
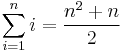











![\sum_{n=s}^t f(n) + \sum_{n=s}^{t} g(n) = \sum_{n=s}^t \left[f(n) + g(n)\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/207fc076b9b57a8845852e18ab6bfe8f.png)
![\sum_{n=s}^t f(n) - \sum_{n=s}^{t} g(n) = \sum_{n=s}^t \left[f(n) - g(n)\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/f46bc18b95a08cf74305e78855602b8f.png)




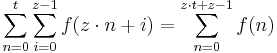

![c^{\left[\sum_{n=s}^t f(n) \right]} = \prod_{n=s}^t c^{f(n)}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bbf5714f69ebad66b81ea4f0c6e99000.png)

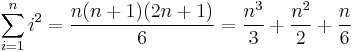
![\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^4}{4} + \frac{n^3}{2} + \frac{n^2}{4} = \left[\sum_{i=1}^n i\right]^2](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6bc8ee6ceae64e42253d2684a8632803.png)